Escenarios envolventes, personajes vivos, efectos alucinantes… Los gráficos hacen cada vez más difícil discriminar qué es ficción en los videojuegos, y la clave para conseguirlo son, lo creas o no, las matemáticas.
Nos hemos acostumbrado a que los videojuegos hagan gala de unos gráficos cada vez más espectaculares, y todo parece indicar que la progresión es imparable. No parece demasiado lejano el momento en que se nos haga muy difícil diferenciar los gráficos de la imagen real. Las últimas versiones de Unreal Engine y CryEngine consiguen un realismo gráfico nunca visto, y permiten ver efectos que hasta hace poco eran imposibles de realizar en tiempo real. ¿Alguna vez te has preguntado de qué forma se representan esos gráficos alucinantes en tu monitor? En esta entrega del Taller nos introduciremos en los fundamentos matemáticos que hacen esto posible.

Triángulos
Aunque es posible utilizar otros elementos, las tarjetas gráficas de nuestros ordenadores trabajan principalmente con un tipo de figura geométrica: el triángulo, el más elemental de los polígonos. La superficie de los objetos tridimensionales que aparecen en los videojuegos, llamada malla, está formada por triángulos, incluso aunque hoy sea difícil percatarse de ello a simple vista. Conectando triángulos se consiguen mallas con volumen, y podemos definir figuras con prácticamente cualquier forma. Los vértices que definen los triángulos de una malla requieren de tres coordenadas (X, Y y Z) que definen su posición en el espacio tridimensional.
Coordenadas homogéneas
La mayoría de sistemas de representación gráfica por computador utilizan un sistema de coordenadas homogéneas. Este sistema fue introducido por el matemático alemán August Ferdinand Möbius, en 1837. En el espacio tridimensional, un sistema homogéneo utiliza cuatro coordenadas en lugar de tres para definir un punto. Estas coordenadas son X,Y,Z y W. Como habíamos visto anteriormente, el espacio tridimensional –también llamado espacio euclídeo– consta de tres coordenadas, «XYZ». Para obtener las coordenadas «XYZ» del espacio euclídeo, dividimos las coordenadas «XYZ» homogéneas por «W». Así, un punto definido por la coordenadas homogéneas (15, 8, 6, 1) se encuentra en el punto (15/1, 8/1, 6/1) = (15, 8, 6) del espacio euclídeo. En este caso, al tener «W» el valor 1, las coordenadas «XYZ» homogéneas coinciden con las coordenadas «XYZ» del espacio euclídeo. Aunque W podría tener cualquier valor, en computación gráfica utilizaremos únicamente los valores 0 y 1.
Sólo aplicando las abstractas matemáticas es posible lograr el realismo más «tangible»
Si cogemos el ejemplo anterior dando a «W» el valor 0, obtenemos que el punto definido por las coordenadas homogéneas (15, 8, 6, 0) se encuentra en el punto (15/0, 8/0, 6/0) = (∞, ∞, ∞). Esta es una de las características de un sistema de coordenadas homogéneas: permite definir los llamados puntos impropios o del infinito, que son puntos que se encuentran fuera de nuestro espacio tridimensional.

En computación gráfica, se utiliza la «W» con valor 1 para definir un punto del espacio, y la «W» con valor 0 para definir una orientación. Se trata de un vector que no define un punto, sino una dirección desde el origen de coordenadas, y se emplea para realizar rotaciones.
Matrices
Desempolvemos un poco las matemáticas del instituto. Recordemos que una matriz es una colección de valores distribuidos en una serie de filas y columnas. Tiene múltiples usos, el más típico que se enseña en secundaria es el de facilitar la resolución de sistemas de ecuaciones. En nuestro caso, las matrices son muy útiles para poder definir transformaciones con coordenadas homogéneas. Podemos codificar en una matriz cuadrada de orden 4 (es decir, con 4 filas y 4 columnas) la traslación, rotación y escala de un elemento.
Existen diferentes formas de representar las transformaciones en una matriz, y según la librería gráfica que utilicemos se definirán de una forma u otra. En este artículo vamos a guiarnos por la forma en que codifica la información OpenGL, un estándar para la creación de gráficos por computador disponible en múltiples plataformas. Hoy día incluso se pueden realizar gráficos 3D para la web con una versión de esta librería, WebGL.
En el arcade Geometry Wars, aunque se desarrolla casi siempre en planos bidimensionales, permite apreciar de un modo más directo transformaciones geométricas. Todas ellas emplean matrices.
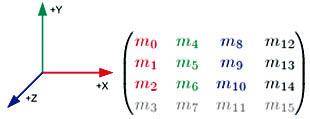
Habíamos dicho que las coordenadas «XYZ» de un vector representan su desplazamiento desde el origen de coordenadas, en el caso de que se trate de un punto en el espacio (es decir, si su coordenada homogénea «W» es 1), o una orientación (si su coordenada «W» es 0). En OpenGL, la información del sistema de coordenadas se codifica de la siguiente forma:
La primera columna especifica la dirección del eje «X». Al ser una dirección, su «W» (el elemento m3) valdrá 0. Las columnas segunda y tercera contienen la dirección de los ejes «Y» y «Z», respectivamente, con lo que su valor «W» será igualmente 0. La última columna contiene información sobre la traslación definida en la matriz (este último dato, al ser una posición y no una orientación, tiene como valor de «W» 1). Si multiplicamos un vector por esta matriz, obtendremos como resultado un vector transformado según la información de la matriz. Por ejemplo, si en la última columna de la matriz colocamos el vector (5,0,0,1) y multiplicamos la matriz por el punto (10,0,0,1), obtenemos el punto desplazado 5 unidades hacia la derecha, es decir, en las coordenadas (15,0,0,1). Esto nos resultará muy útil para el siguiente apartado.
Espacio y su proyección
Hasta ahora, hemos estado hablando siempre del espacio tridimensional en el que representamos nuestros objetos, pero cuando vemos nuestro juego en el monitor, realmente lo estamos viendo sobre un dispositivo plano, que no tiene tres dimensiones, sino dos. A la conversión de todos los elementos tridimensionales en objetos visibles en el plano de la pantalla se le llama proyección. Para realizar esta proyección de la escena a la pantalla, utilizaremos nuevamente multiplicación de matrices.

La representación en la pantalla de cada una de las mallas de triángulos de nuestro juego consta de varios pasos. En primer lugar, pasaremos del espacio local al espacio de la escena; después, al espacio del observador; y por último, al espacio proyectado sobre la pantalla. Pasaremos a explicar en qué consiste cada uno de estos pasos.
Los fundamentos de geometría son esenciales para el diseño de cualquier videojuego, 2D o 3D
Como habíamos dicho que un objeto puede moverse libremente por la escena utilizando operaciones con matrices, no podemos definir las coordenadas de los vértices de sus triángulos respecto de la escena, ya que esas coordenadas variarán al moverse. Por eso, los vértices se definen en las llamadas coordenadas locales, que son independientes de la posición del objeto en la escena. Esto significa que si en nuestro juego aparecen varios objetos idénticos, las coordenadas de sus vértices son iguales en todos ellos. Pero, ¿cómo pueden tener las mismas coordenadas si aparecen en puntos diferentes del espacio? Pues es porque crearemos una matriz de transformación diferente para cada uno de ellos, y multiplicaremos los vértices de cada uno por sus respectivas matrices. El resultado serán las coordenadas de cada vértice en el espacio de la escena, y ya no coincidirá entre todos los objetos.

Ahora, incluso aunque estos objetos no se muevan, cuando la cámara que sigue al jugador se mueve por la escena, los objetos se van desplazando por la pantalla, con lo que es obvio que con la obtención de las coordenadas de escena no tenemos información suficiente, ya que la representación final no depende tan sólo de la posición de cada objeto en la escena, sino también de la de la cámara. Así que, la transformación de la cámara se definirá en una nueva matriz, y multiplicaremos los vértices en coordenadas de escena por dicha matriz, obteniendo las coordenadas de cada vértice en el espacio del observador.

Ya sólo nos queda un último paso: todas estas transformaciones nos siguen dando coordenadas en el espacio tridimensional, y es necesario convertirlas en coordenadas sobre la pantalla, para saber dónde hay que dibujar finalmente cada elemento. Esto se hace con una última matriz, cuyos datos se definen de una forma un tanto diferente a las vistas anteriormente, y que se llama matriz de proyección. Al multiplicar cada vértice por esta matriz, nos da sus coordenadas de pantalla. Así, ahora la escena puede dibujarse en tu monitor.
ESPACIO EUCLÍDEO

Las mallas representan objetos en el espacio 3D, también llamado espacio euclídeo. Cada objeto tiene una posición en este espacio tridimensional, y es posible rotarlo y cambiarlo de tamaño. Su posición es el desplazamiento del objeto con respecto al origen de la escena. El origen de la escena es el punto (0,0,0), siendo cada uno de estos valores sus coordenadas «X», «Y» y «Z» respectivamente.
Se puede configurar el sistema de coordenadas de muchas formas. Una habitual es que el eje X representa el desplazamiento a izquierda y derecha, el eje Y hacia arriba y abajo, y el eje Z hacia adelante y atrás. Por ejemplo, un objeto situado en las coordenadas (5, 0, 0) se encuentra desplazado 5 puntos a la derecha sobre el origen.



Definir la posición y orientación en los objetos en espacios 3D pueden dar lugar a paradojas imposibles… O a magníficas ficciones como la de Portal 2. En la otra pantalla, cada vértice de un triángulo en el espacio tridimensional consta con tres datos relativos a los ejes de coordenadas X, Y y Z que lo sitúan en un punto en concreto. Todos los escenarios de cualquier videojuego están construidos a partir de una estructura de malla como la que ves en la imagen.
ROTACIONES
La especificación de rotaciones es uno de los aspectos más complejos de la programación de gráficos en tres dimensiones. Como se menciona arriba, la orientación de los elementos se define en las primeras tres columnas de la matriz, pero no se suele trabajar directamente con estos datos. Se busca una forma de definir rotaciones más compacta y que permita realizar operaciones lo más rápido posible, sobre todo cuando debemos combinar e interpolar varias rotaciones, por ejemplo para el cálculo de animaciones. Una vez hechas todas las operaciones, se codifican los datos en la matriz.
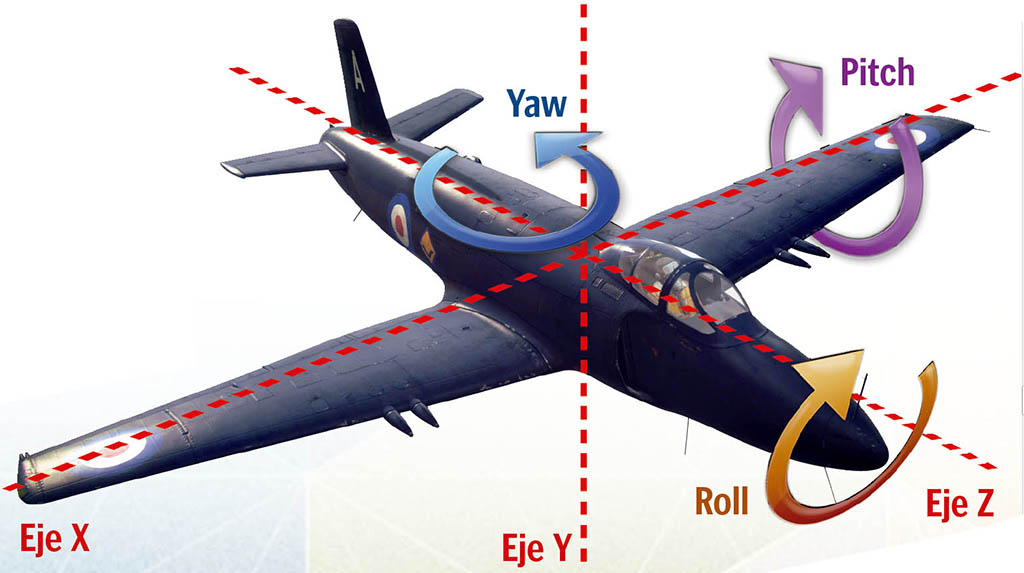
Una forma de representar las rotaciones es el uso de rotaciones Euler, enunciado por el matemático del mismo nombre. Este sistema es muy sencillo: definimos la orientación de un objeto especificando una rotación (en grados o radianes) sobre cada uno de los ejes «X», «Y» y «Z» de nuestro sistema de coordenadas. A la rotación sobre cada uno de estos ejes se le demina con las palabras inglesas pitch, yaw y roll, respectivamente.
En cambio, existen varios problemas con este sistema: la interpolación de dos rotaciones no es trivial, siempre existen dos maneras de representar una misma orientación, el orden en que se rota sobre cada eje da orientaciones finales diferentes, y se puede producir el bloqueo del cardán (gimbal lock), que hace que, en determinadas ocasiones, rotar sobre dos ejes diferentes produce exactamente la misma orientación.
Por ello, normalmente los motores gráficos implementan otro sistema para representar rotaciones, los llamados cuaterniones. La explicación de los cuaterniones no es sencilla y va mucho más allá del propósito de este artículo. Se trata de una extensión de los números reales (similar a los números complejos) y cuyas propiedades los convierte en una forma muy eficiente de almacenar información sobre rotaciones en el espacio tridimensional.
 El EXPERTO
El EXPERTO
Javier San Juan Cervera Co-director del Máster en Programación de videojuegos U-tad.
- Javier San Juan Cervera ha trabajado como programador de videojuegos en Digital Jokers y Future World Games, así como desarrollador freelance de aplicaciones de iOS, e investigador en materia de Inteligencia Artificial en la Universidad Politécnica de Madrid.
- En la actualidad es profesor en U-tad, y Co-director del Máster en Programación de videojuegos en ese mismo centro junto a Jon Beltrán de Heredia.